Le but de cet exercice est de travailler les pointeurs (et les structures) sur une notion très connue en informatique pour organiser les données : les listes chaînées.
Cliquez ici si vous souhaitez faire cet exercice.
Un petit exercice simple pour manipuler les références (C++) comme référencement d'objets (cas d'utilisation numéro 1 du cours).
Créez une structure Maison contenant simplement une adresse (chaîne de caractères).
Créez ensuite une structure Personne contenant un nom (chaîne de caractères) et une référence sur une Maison.
Les différents habitants d'une maison n'ont en effet pas une copie de leur maison avec eux, mais simplement un moyen d'y référer (mémoire de l'adresse)...
C'est un cas typique d'illustration des références.
Créez ensuite deux maisons différentes dans le main(), puis créez des personnes différentes habitant dans des maisons différentes (plusieurs habitants par maison).
La principale difficulté réside dans le fait qu'une référence doit toujours référencer quelque chose : il faut donc affecter les maisons dès l'initialisation.
Pour finir cette partie : créez une fonction affiche qui affiche une personne en indiquant son nom et son adresse, par exemple :
Pierre habite 12 rue du Château
Affichez toutes les personnes de votre programme.
Le cadre choisi ici illustre aussi les limites des références : avec cette implémentation, il est impossible à une personne de déménager : on ne peut en effet pas «changer de référence».
C'est parfait si c'est vraiment ce que l'on veut dans le programme (=on est sûr que personne ne déménagera).
Mais si l'on voulait pouvoir faire déménager les personnes, il faudrait faire autrement... à vous de trouver comment.
En clair : implémenter une seconde version du programme dans laquelle vous faites déménager au moins une personne.
Assurez-vous que les autres personnes à la même (ancienne) adresse n'ont pas elles aussi déménagé (ce qui serait le cas avec des références :-( ).
Un petit exercice simple pour manipuler les pointeurs comme sélecteurs d'objets.
Créez un nouveau fichier appelé selecteur.cc.
Dans le main(), créez trois variables valeur1 valeur2 et valeur3, de type double que vous
initialisez à des valeurs de votre choix.
Déclarez un pointeur choix, pointeur sur des double.
Demandez ensuite un nombre entre 1 et 3 à l'utilisateur (cf exercice 2 série 5) et, en fonction de son choix, faites pointer choix sur valeur1, valeur2 ou valeur3.
Pour finir affichez Vous avez choisi et la valeur choisie en utilisant le pointeur choix.
Remarque : il est évident que le but de cet exercice n'est que de manipuler les pointeurs. Hors de ces contraintes, la bonne solution pour faire la même chose serait bien sûr d'utiliser un tableau.
On s'intéresse ici au problème suivant :
étant donnée une liste (finie) de nombres entiers, positifs et
négatifs, trouver la sous-liste (contiguë) de somme maximale.
Par exemple si la liste est :
11, 13, -4, 3, -26, 7, -13, 25, -2, 17, 5, -8, 1la sous-liste 3, -26, 7, -13, 25 a pour somme -4,
25, -2, 17, 5(de somme 45).
Un des objectifs de cet exercice est de travailler les pointeurs (qui ne sont pas strictement nécessaire pour résoudre ce problème).
Un autre objectif est de revenir sur la complexité des algorithmes et comparer différentes versions de solutions.
Pour résoudre informatiquement ce problème définissez les types suivants :
Valeur, pour représenter les valeurs de la liste (int ici);
Liste, pour représenter une liste de valeurs;
Somme_sous_liste comme une structure comprenant :
Pour tester, commencer de suite à déclarer dans le main() un tableau de listes, p.ex. :
vectorseq({ { 11, 13, -4, 3, -26, 7, -13, 25, -2, 17, 5, -8, 1 }, {}, { -3, -4, -1, -2, -3 }, { -1, -4, -3, -2, -3 }, { 3, 4, 1, 2, -3 }, { 3, 4, 1, 2, 3 }, { 3, -1, -1, -1, 5 }, { -5, -4, 1, 1, 1 } });
L'algorithme le plus simple qui vient à l'esprit est de chercher parmi toutes les sous-listes, celle de somme maximale. « Chercher parmi toutes les sous-listes » signifie, pour tous les débuts possibles, et pour toutes les fins possible pour un tel début.
D'où l'algorithme suivant :
Entree : liste de N nombres
Sortie : la sous-liste (debut, fin, somme) de somme maximale
sousliste = (0, 0, -infini)
Pour tout debut de 1 à N
Pour tout fin de debut à N
somme = 0
Pour tout position de debut à fin
somme = somme + liste[position]
Si somme > sousliste.somme
sousliste = (debut, fin, somme)
Sortir : sousliste
QUESTION : quelle est la complexité de cet algorithme ?
Implémentez cet algorithme (en C++) dans une fonction tranche_max_1 (de votre programme tranches.cc).
Complétez la fonction main() pour rechercher la sous-liste (ou « tranche ») de somme maximale dans vos listes de test.
La complexité de l'algorithme précédent vient de ses boucles imbriquées.
Serait-il possible d'en enlever une ?
En regardant de plus prêt, on s'appercoit vite que l'on refait
beaucoup de calculs plusieurs fois :
le calcul de la somme
d'une sous-liste utilise souvent les calculs d'une sous-liste
précédente.
En d'autres termes, la boucle la plus intérieure est inutile car pour calculer la somme à « position+1 », il suffit d'ajouter liste[position+1] à l'ancienne somme.
Voici alors un nouvel algorithme :
Entree : liste de N nombres
Sortie : la sous-liste (debut, fin, somme) de somme maximale
sousliste = (0, 0, -infini)
Pour tout debut de 1 à N
somme = 0
Pour tout fin de debut à N
somme = somme + liste[fin]
Si somme > sousliste.somme
sousliste = (debut, fin, somme)
Sortir : sousliste
QUESTION : quelle est la complexité de cet algorithme ?
Implémentez cet algorithme dans une fonction tranche_max_2 et vérifiez qu'il fournit les bons résultats.
Peut-on aller plus loin ? Peut-on encore enlever une boucle ?
La réponse est oui, mais la solution est peut-être moins triviale.
L'idée reste cependant la même : supprimer des calculs inutiles. Mais elle utilise ici le fait que l'on cherche un maximum.
Si donc on trouve une sous-liste initiale de somme inférieure (ou égale) à 0, on peut supprimer cette sous-liste initiale car elle apporte moins à la somme totale que de commencer juste après elle.
Par exemple dans la liste 4,-5,3,... il vaut mieux commencer au 3 (avec une somme initiale qui vaut 0) que commencer au 4 (qui nous donne une somme de -1 arrivé au 3).
D'où l'idée de l'algorithme suivant :
Entree : liste de N nombres
Sortie : la sous-liste (debut, fin, somme) de somme maximale
sousliste = (0, 0, -infini)
debut = 1
somme = 0
Pour tout fin de 1 à N
somme = somme + liste[fin]
Si somme > sousliste.somme
sousliste = (debut, fin, somme)
Si somme <= 0
debut = fin + 1
somme = 0
Sortir : sousliste
QUESTION : quelle est la complexité de cet algorithme ?
Implémentez cet algorithme dans une fonction tranche_max_3 et vérifiez qu'il fournit les bons résultats.
Vous pouvez aussi :
vous aider d'une fonction affiche() pour afficher les résultats ;
(semaine prochaine) lire des listes depuis un fichier.
Le but est ici de faire un programme capable de dériver formellement des expressions (arithmétiques).
On utilisera pour cela une structure d'arbre binaire. Un
arbre binaire est une structure de donnée définie de façon récursive par :
un arbre est
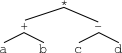
Par exemple, si l'on note un arbre entre parenthèses, en premier son sous-arbre droit, puis sa valeur et enfin son sous-arbre gauche, alors
(((a) + (b)) * ((c) - (d)))
est un arbre binaire : la valeur est * et les deux sous-arbres ((a) + (b)) et ((c) - (d)) :

De même (a) est un arbre réduit à une valeur (c.-à-d. avec 2 sous-arbres vides).
Dans cette structure de données, la valeur sera représentée par un char.
Assurez-vous que l'arbre puisse partager un
ou plusieurs sous-arbres. Par exemple, l'arbre ((x) + (x))
peut être construit à partir d'un seul arbre (x). Pour ce faire, vous
utiliserez un compteur de références c.-à-d. un nombre qui compte combiens d'arbres utilisent un sous-arbre donné (les plus avancés d'entre vous pourront utiliser ici un shared_ptr, hors du programme du cours).
On affichera récursivement le sous-arbre de gauche, puis la valeur puis (récursivement) le sous arbre de droite.
On utilisera pour cela les arbres binaires (nous ne considérerons ici
que les opérateurs binaires + - / * et ^
(puissance)) :
par
exemple
a + b sera représenté par l'arbre
((a) +
(b))
où '+' est la valeur
du premier arbre et "(a)" et "(b)" ses sous-arbres.
De même, l'expression arithmétique
(a + b) * (c + d)
sera
représentée par l'arbre
(((a) + (b)) * ((c) + (d)))
Construire les arbres
représentant les expressions suivantes (4 expressions) :
x + a
(x + a) * (x + b)
((x * x) * x) + (a * x)
(x ^ a) / ((x * x) + (b * x))
Indication : commencez par créer les arbres binaires représentant les expressions a, b et x (seuls), puis ceux représentant les expressions x+a, x+b et x*x.
On procédera pour cela de façon récursive en se rappelant les règles usuelles de dérivation :
da/dx = 0 où a est une constante (ici : caractère différent de x) dx/dx = 1 d(f+g)/dx = df/dx + dg/dx d(f-g)/dx = df/dx - dg/dx d(f*g)/dx = (df/dx * g) + (f * dg/dx) d(f/g)/dx = ((df/dx * g) - (f * dg/dx) ) / (g * g) d(f^a)/dx = a * df/dx * (f ^ (a - 1)) (où a ne dépend pas de x, ce que l'on supposera ici)Note importante : on ne veut pas l'arbre minimal de dérivation ! En clair, on ne cherchera pas à simplifier les expressions obtenues.