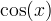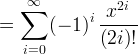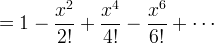Série 5 :
Fonctions (1)
But
Le but de cette série d'exercices est de vous faire
pratiquer les fonctions en C++ : prototypage, définition,
appel...
Préliminaires :
Avant d'effectuer les manipulations décrites dans cette série,
créez le répertoire ~/Desktop/myfiles/cpp/serie05 (i.e.
créez le sous-répertoire serie05 dans le
répertoire ~/Desktop/myfiles/cpp).
Exercice 0 : reprise de l'exemple du cours (fonctions, niveau 0)
Cet exercice est disponible en page 27 de l'ouvrage C++ par la pratique
Exercice tutoriel semaine 4 du MOOC
Le but de cet exercice est de reprendre l'exemple du cours
illustrant l'utilisation de fonctions.
Cliquez ici si
vous souhaitez faire cet exercice.
Exercice 1 : Portée (niveau 1)
Exercice n°12 (pages 30 et 209) de l'ouvrage C++ par la pratique.
Copiez (avec la souris : sélectionnez le texte puis cliquez
le bouton du milieu dans Emacs) le contenu suivant dans un fichier
portee.cc et compilez-le (ne prêtez pas attention
aux «Warnings») et lancez l'exécution.
#include <iostream>
using namespace std;
int variable(10);
int main()
{
{
int variable(5);
cout << "Un, la variable vaut : " << variable << endl;
}
{
cout << "Deux, la variable vaut : " << variable << endl;
}
for (int variable(0); variable < 3; ++variable) {
cout << "Trois, la variable vaut : " << variable << endl;
}
cout << "Quatre, la variable vaut : " << variable << endl;
for (variable = 0; variable < 3; ++variable) {
cout << "Cinq, la variable vaut : " << variable << endl;
}
cout << "Six, la variable vaut : " << variable << endl;
return 0;
}
- Quelles sont les variables locales et globales pour chaque bloc ?
- Expliquez [à votre voisin(e)] les valeurs affichées.
Exercice 2 : Prototypes (niveau 1, puis 2 pour les points 4 & 5)
Exercice n°12 (pages 31 et 210) de l'ouvrage C++ par la pratique.
Exercice n°11 du MOOC (semaine 4)
Écrivez un programme proto.cc dans lequel vous
définissez une fonction demander_nombre()
respectant le prototype suivant :
int demander_nombre();
Cette fonction doit demander à l'utilisateur un entier et le renvoyer.
-
Placez la définition de la fonction avant le main().
Faites appel à la fonction dans le main() et
affichez le résultat renvoyé.
-
Que se passe-t-il si l'on déplace la définition de
la fonction demander_nombre() après le
main() et que l'on recompile le
programme ?
(faites-le et vérifiez si le compilateur réagit comme
vous vous y attendiez).
-
Ajoutez ensuite le prototype de la fonction
demander_nombre() avant
main() et recompilez le programme.
-
Modifiez maintenant la fonction pour qu'elle prenne 2
arguments : les bornes minimales et maximales entre lesquelles
l'utilisateur doit donner le nombre.
La fonction doit boucler tant que l'utilisateur ne donne pas un chiffre valide.
-
Raffinez encore le programme de sorte que si la borne maximale
est inférieure ou égale à la borne minimale, elle ne soit pas prise
en compte (c'est-à-dire que l'on peut entrer n'importe quel chiffre
plus grand que la borne minimale).
Exercice 3 : Fonctions simples (niveau 1)
Exercice supplémentaire n°7 du MOOC (semaine 4)
Écrivez les fonctions suivantes, et testez-les en les appelant dans la fonction main de votre programme sur des exemples:
- Écrivez une fonction
min2 qui reçoit deux arguments de type double et retourne le plus petit d'entre eux. Le type de retour devra donc être double.
- Écrivez une fonction
min3 qui prend trois arguments de type double et retourne le plus petit d'entre eux. Comment utiliser la fonction min2 du point précédent pour écrire le corps de min3 en une ligne ?
Exercice 4 : Passage des paramètres (niveau 1)
Exercice n°13 (pages 31 et 212) de l'ouvrage C++ par la pratique.
Exercice n°11 du MOOC (semaine 4)
Écrivez le programme echange.cc dans lequel vous
devez écrire (prototype + définition) une fonction
echange qui :
- accepte deux arguments de type entier ;
- échange les valeurs de ces deux arguments.
Vous essayerez votre fonction avec le code
main suivant :
int main()
{
int i(10);
int j(55);
cout << "Avant: i=" << i << " et j=" << j << endl;
echange(i,j);
cout << "Après: i=" << i << " et j=" << j << endl;
return 0;
}
Si votre fonction est correcte, le programme affichera:
Avant: i=10 et j=55
Après: i=55 et j=10
Exercice 5 : Sapin (niveau 2)
Exercice supplémentaire n°8 du MOOC (semaine 4)
On vous donne les deux fonctions suivantes:
void etoiles(int nb_etoiles)
{
for(int i(0); i < nb_etoiles; ++i) {
cout << '*';
}
}
void espaces(int nb_espaces)
{
for(int i(0); i < nb_espaces; ++i) {
cout << ' ';
}
}
- Utilisez ces fonctions pour écrire une fonction qui affiche un triangle d'étoiles, et qui prend en paramètre le nombre de lignes du triangle:
*
***
*****
- Utilisez cette fonction pour afficher un sapin:
*
***
*
***
*****
*
***
*****
*******
*
Vous devrez modifier un peu la fonction écrite au point 1. afin que votre sapin ressemble à celui dessiné ci-dessus.
-
Le sapin précédent n'est pas très joli. Il est bien trop allongé et ne ressemble pas beaucoup à un vrai sapin. Adaptez votre code pour qu'il affiche le graphique ci-dessous:
*
***
*****
***
*****
*******
*****
*******
*********
|||
Exercice 6 : calcul de PGDC
(algorithme d'Euclide, niveau 1)
Exercice n°38 (pages 90 et 272) de l'ouvrage C++ par la pratique.
(pages 92 et 272 dans la 2e édition).
(PGDC = plus grand diviseur commun)
Buts
Écrivez le programme pgdc.cc qui :
- demande à l'utilisateur d'entrer deux entiers strictement
positifs a et b;
- teste si a et b sont bien strictement
positifs, et dans le cas
contraire les redemande à l'utilisateur.
- trouve les entiers u, v et p satisfaisant
l'identité de
Bezout (i.e. une équation à valeurs entières) : u a + v b = p,
avec p le plus grand commun diviseur de a et b.
Méthode
La méthode utilisée est l'algorithme d'Euclide.
On procédera par itération, comme suit (en notant x / y le
quotient et
x % y le reste de la division entière de x par y) :
| 0 : initialisation |
|
|
u0 = 1 |
v0 = 0 |
|
x1 = a |
y1 = b |
u1 = 0 |
v1 = 1 |
|
... |
... |
... |
... |
| i+1 : itération |
xi+1 = yi |
yi+1 = xi % yi |
ui+1 = ui-1 -
ui(xi / yi) |
vi+1 = vi-1 -
vi(xi / yi) |
|
... |
... |
... |
... |
| Valeurs finales |
xk-1 |
yk-1 != 0 |
uk-1 |
vk-1 |
| k : condition d'arrêt quand yk = 0 |
p = xk |
yk = 0 |
inutile |
inutile |
C'est-à-dire que l'on va calculer de proche en proche les valeurs
de x, y, u et v. En calculant
à chaque fois les nouvelles valeurs en fonction des anciennes (et
en faisant bien attention à mémoriser ce qui est nécessaire à un
calcul correct, voir
les indications ci-dessous).
Par exemple, yi+1 = xi % yi
veut dire : "la nouvelle valeur de y vaut l'ancienne
valeur de x modulo l'ancienne valeur de y".
Programmez ces calculs dans une boucle, qui s'execute tant que la
condition d'arrêt n'est pas vérifiée.
Pensez à initialiser correctement vos variables avant d'entrer
dans la boucle.
Indications
Vu les dépendances entre les calculs, vous aurez besoin de définir (par exemple) les variables :
x, y,
u, v et q=x/y, r=x%y, prev_u,
prev_v, new_u et new_v.
Vous mettrez ces
variables à jour à chaque itération, à l'aide des formules de la ligne
i+1 et des relations temporelles évidentes entre elle
(par exemple prev_u = u).
Testez si y est non nul avant d'effectuer les divisions !
Exemple d'execution
Entrez un nombre entier supérieur ou égal à 1 : 654321
Entrez un nombre entier supérieur ou égal à 1 : 210
Calcul du PGDC de 654321 et 210
x y u v
210 171 1 -3115
171 39 -1 3116
39 15 5 -15579
15 9 -11 34274
9 6 16 -49853
6 3 -27 84127
3 0 70 -218107
PGDC(654321,210)=3
Notes
-
Vous pouvez réutiliser la fonction
demander_nombre() de
l'exercice 11 de la semaine 4 du MOOC (semaine 5 d'ICC).
- Remarquez que pour le seul calcul du PGDC, le calcul de
x et y par l'algorithme ci-dessus suffit, pas
besoin de u et v. Ils ont été introduits ici pour résoudre
l'équation de Bezout (et vous faire programmer des suites
imbriquées). Par exemple sur l'exemple précédent on a :
-27 * 654321 + 84127 * 210 = 3.
Exercice 7 : La fonction cosinus (définition et appel de
fonction, niveau 2)
Exercice n°14 (pages 32 et
213) de l'ouvrage C++ par la pratique.
Exercice n°13 du MOOC (semaine 4)
Le but de cet exercice est d'écrire un programme cos.cc qui calcule une
approximation de la fonction cosinus cos(x) (pour x dans [0, 2*pi])
Méthode
Pour calculer cos(x), on utilisera son développement en série :
Tâches
Écrire les fonctions suivantes (qui seront ensuite appelées depuis le main()) :
-
double factorielle(int k)
qui calcule la factorielle d'un nombre k
(et la retourne au format double)
Utilisez pour cela une boucle for.
-
double somme_partielle(double x, int N)
qui calcule la somme partielle de la série au rang N
(somme des N premiers termes de la série ci-dessus).
Ensuite, dans le main() :
demander une valeur de N à l'utilisateur (vous pouvez utiliser ici la fonction
demander_nombre de l'exercice 2), puis demander une valeur de x et tant
que l'utilisateur n'entre pas 0.0, le programme calcule et affiche la valeur approchée
du cosinus du nombre entré, en utilisant les fonctions précédentes..
Remarques :
-
La fonction factorielle renvoie facilement
des nombres très grands, qui dépassent les capacités de précision de
l'ordinateur. Pour un ordre de grandeur, avec le type double,
la plus grande valeur permise sera 170 (170! = 7.25742e+306).
La valeur retournée pour des nombre supérieurs à ces valeurs
limites sera Infinity.
Évitez donc de tester le programme avec de trop grandes valeurs de N.
-
Vous pouvez raffiner votre programme de sorte à garantir que N soit
inférieur ou égal à 85 (par exemple en utilisant la borne maximale
dans demander_nombre).
-
Notez que pour afficher plus de décimales dans le résultat, vous
pouvez utiliser cout.precision, par exemple :
cout.precision(12);.
Dernière mise à jour le 8 septembre 2021
Last modified: Wed Sep 8, 2021
|