Série 7 :
Tableaux dynamiques

Préliminaires :

Exercice 0 : Manipulation d'un tableau dynamique (niveau 0)

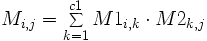
Le but de cet exercice est d'illustrer l'utilisation d'un tableau dynamique.

Cliquez ici si vous voulez faire cet exercice.

Exercice 1 : Échauffement avec les tableaux dynamiques (niveau 1)

Rappel : Pour utiliser le type vector, il faut inclure la librairie définissant ce type, au moyen de la directive :

#include <vector>

En vous aidant si nécessaire d'un programme, répondez aux questions suivantes :

A : Quelles valeurs contient le tableau tab après l'exècution des lignes suivantes ? Expliquez.

constexpr size_t taille(10);
vector<size_t> tab;
for (size_t i(0); i < taille; ++i) {
    tab.push_back(tab.size());
}

B : Que fait la fonction f suivante ?

void f(vector<int>& tab, vector<int>& tab2)
{
    for (size_t i(0); i < tab.size(); ++i) {
        tab2.push_back(tab[0]);
    }
}

Exercice 2 : Produit scalaire (tableaux dynamiques, niveau 1)

Écrivez un programme scalaire.cc qui calcule le produit scalaire de deux vecteurs, implémenté au moyen de tableaux dynamiques.

Votre programme devra utiliser (entre autres) les éléments suivants :

• deux variables de type tableau dynamique de réels ;
• une fonction qui calcule le produit scalaire : double scalaire(vector<double> u, vector<double> v);

• demander à l'utilisateur d'entrer n, la taille effective des vecteurs.
• demander à l'utilisateur les composantes (v1₀... v1_n-1 , v2₀ ... v2_n-1) des vecteurs v1 et v2.
• appeler la fonction scalaire(...) pour calculer le produit scalaire de v1 et v2.
• afficher le résultat.

Rappel :
Le produit scalaire de a par b est: a.b = a₁*b₁ + a₂*b₂ + ... + a_n*b_n

Exemple: a = (5, 3, -1)   b = (2, 1, 2)    a.b = 11

Exercice 3 : Multiplication de matrices (tableaux dynamiques, niveau 2)

On cherche ici à écrire un programme mulmat.cc qui calcule la multiplication de deux matrices (rappel ci-dessous).

Vous utiliserez pour représenter la matrice un vecteur de vecteurs de doubles.

Déclarations :

• dans main(), déclarez deux matrices M1 et M2.

Fonctions :

• la fonction de prototype

  vector<vector<double>> lire_matrice();

  qui lit depuis le clavier les éléments d'une matrice (après avoir demandé sa taille) et retourne la matrice résultante.
• la fonction de prototype

  vector<vector<double>> multiplication(const vector<vector<double>>& Mat1,
                                        const vector<vector<double>>& Mat2);

  qui multiplie deux matrices de tailles compatibles et renvoie le résultat.
• la fonction de prototype

  void  affiche_matrice(const vector<vector<double>> M);
    

  qui affiche le contenu d'une matrice ligne par ligne.

Méthode :

• lire depuis le clavier les dimensions l1 (nombre de lignes) et c1 (nombre de colonnes) de la première matrice M1
• lire le contenu de M1.
• De même, lire les dimensions puis le contenu de la seconde matrice M2.
• Vérifier que le nombre de lignes de M2 est identique au nombre de colonnes de M1.
  Dans le cas contraire, afficher un message d'erreur «Multiplication de matrices impossible !».
• Effectuer la mutliplication des matrices : M = M1*M2 :
  • Les dimensions de M sont : l1 (nombre de lignes) et c2 (nombre de colonnes).
  • l'élément M_i,j est défini par
• afficher le résultat ligne par ligne.

Exemple d'utilisation :

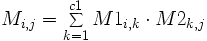
Saisie d'une matrice :
  Nombre de lignes : 2
  Nombre de colonnes : 3
  M[1,1]=1
  M[1,2]=2
  M[1,3]=3
  M[2,1]=4
  M[2,2]=5
  M[2,3]=6
Saisie d'une matrice :
  Nombre de lignes : 3
  Nombre de colonnes : 4
  M[1,1]=1
  M[1,2]=2
  M[1,3]=3
  M[1,4]=4
  M[2,1]=5
  M[2,2]=6
  M[2,3]=7
  M[2,4]=8
  M[3,1]=9
  M[3,2]=0
  M[3,3]=1
  M[3,4]=2
Résultat :
38 14 20 26
83 38 53 68

Exercice 4 : Éléments en indice (niveau 2)

Écrivez une fonction appelée elements_en_indice prenant un tableau T d'entiers en paramètre. La fonction devra retourner un nouveau tableau, qui sera construit de la façon suivante : Les éléments de T d'indice pair seront placés dans ce nouveau tableau à l'indice donné par l'élément suivant de T:

• T[0] sera placé dans le nouveau tableau à l'indice T[1],
• T[2] sera placé dans le nouveau tableau à l'indice T[3],
• etc...

Testez votre fonction avec le code:

vector<int> A( { 4, 2, 8, 0, 7, 1 } );

for(auto el : elements_en_indice(A) ) {
  cout << el << " ";
}
cout << endl;

Exercice 5 : Crible d'Ératosthène (niveau 2)

Un nombre est dit premier s'il admet exactement 2 diviseurs distincts (1 et lui-même). 1 n'est donc pas premier.

Le crible d'Ératosthène est une méthode de recherche des nombres premiers plus petits qu'un entier naturel n donné. Cette méthode est simple:

• On commence par supprimer tous les multiples de 2 inférieurs à n.
• L'entier 3 n'a pas été supprimé et il ne peut être multiple des entiers qui le précèdent, sinon on l'aurait supprimé; il est donc premier. Supprimons alors tous les multiples de 3 inférieurs à n.
• L'entier 5 n'a pas été supprimé, il est donc premier. Supprimons tous les multiples de 5 inférieurs à n.
• Et ainsi de suite jusque n. Les valeurs n'ayant pas été supprimées sont les nombres entiers plus petits que n.

Écrivez le code qui applique cette méthode pour trouver les nombres premiers inférieurs à 100. Vous devez trouver: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

On utilisera un tableau de booléens :

  vector<bool> supprimes(100, false);

Exercice 6 : LIEN COURS ICC : comparaison de deux tris (niveau 2)

6.1 Tri bulles

Le tri bulles est sûrement le plus simple des tris (il est par contre peu efficace).

L'idée est de parcourir la liste autant fois que nécessaire en échangeant 2 à 2 les éléments consécutifs qui ne sont pas dans le bon ordre.
c'est-à-dire si t[j-1] > t[j], alors on échange t[j-1] et t[j].

L'algorithme est donc le suivant (indices de 1 à taille) :

    Pour i de 1 à taille-1
      Pour j de taille à i+1 (descente)
         Si t[j-1] > t[j]
           échanger t[j-1] et t[j]
    

À faire

1. Dans le fichier tri_bulles.cc, implémentez l'algorithme ci-dessus (attention aux indices en C++ !) dans une fonction tri_bulles prenant comme arguments un tableau d'entiers (statique ou dynamique, au choix)

   Pour échanger deux variables, utiliser la fonction swap fournie par la bibliothèque utility (#include <utility>) : swap(x, y);.

2. Dans la fonction main, déclarez un tableau d'entiers (du même type que choisi ci-dessus) et remplissez-le des éléments

   3, 5, 12, -1, 215, -2, 17, 8, 3, 5, 13, 18, 23, 5, 4, 3, 2, 1

   (18 éléments).

3. Testez votre fonction en affichant le résultat sur le tableau précédent.

4. Effectuez éventuellement d'autres tests (tableau constant, tableau vide ou à 1 élément, tableau déjà trié, tableau trié dans le sens inverse, ...)

Exemple d'exécution

A trier  : 3 5 12 -1 215 -2 17 8 3 5 13 18 23 5 4 3 2 1 
Résultat : -2 -1 1 2 3 3 3 4 5 5 5 8 12 13 17 18 23 215 

Note : Le nom de ce tri vient du fait que les éléments à classer «remontent» à leur place un peu comme les bulles dans un liquide remontent vers la surface.
Ajouter un affichage du tableau à chaque itération pour voir cet effet.

Par ailleurs, on implémente souvent ce tri en remplaçant l'itération « Pour i de 1 à taille-1 » par une itération «Répéter .... tant qu'il y a eu au moins 1 échange ».

6.2 tri de Shell

On cherche ici à implémenter une méthode de tri assez efficace en pratique, surtout pour des tableaux de taille faible à moyenne.
Il s'agit du tri dit « de Shell » du nom de son inventeur.

Le tri de Shell est un tri par insertion à incrément décroissant : au lieu de comparer si un élément est plus petit que son prédecesseur immédiat, on le compare à son prédecesseur à distance k (que l'on fait décroître au cours du temps) ; autrement dit : au lieu d'insérer chaque élément à sa place dans la sous-liste triée de tous les éléments qui le précèdent, on l'insère dans une sous-liste d'éléments qui le précèdent mais distants d'un certain incrément k.

L'algorithme est le suivant (indices de 1 à taille) :

Pour k de taille/2 à 1, en le divisant par 2
    Pour i de k+1 à taille
        j <- i-k
        Tant que j > 0
            Si t[j] > t[j+k]
                échanger t[j] et t[j+k]
                j <- j-k
            Sinon
                j <- 0

Comme pour le tri bulles (partie 6.1), implémentez cet algorithme en C++ (attention aux indices) et testez le sur diverses données.

Attention ! j peut être négatif (par j <- j-k)...

Exemple d'exécution

L'exemple d'exécution est le même que pour le tri bulles ci-dessus.

6.3 lien ICC

On peut montrer que la complexité temporelle pire cas du tri de Shell telle que présenté ici est en O(n^2), mais d'autres stratégies restent possibles pour k et c'est encore une question ouverte (je crois) que de savoir quelle est la meilleure stratégie pour l'évolution de k. On sait par contre que quelque soit la stratégie pour l'évolution de k, la complexité temporelle pire cas est au moins en O(n ( log(n) / log(log(n)) )^2).
Pour plus de détails, voir https://en.wikipedia.org/wiki/Shellsort#Gap_sequences et https://en.wikipedia.org/wiki/Shellsort#Computational_complexity