[retour à la liste des exercices]
Observer de manière concrète comment un nombre entier est converti en une suite de 0 et de 1, et réciproquement.
Pour donner l'écriture binaire d'un nombre entier positif n, il suffit d'appliquer l'algorithme suivant :
Le problème avec l'algorithme ci-dessus est qu'il affiche le nombre à
l'envers. Par exemple pour 2, il affiche 01 au lieu de
10.
Il suffit simplement pour palier ce problème d'utiliser une structure de données auxiliaire dans le langage de programmation choisi (par exemple une chaîne de caractères) et d'y ajouter les symboles 0 ou 1 non pas à la fin comme le ferait un affichage standard, mais au début de la structure de données choisie. Une fois celle-ci remplie, il ne reste plus qu'à l'afficher normalement (c.-à-d. dans l'ordre usuel).
On peut aussi palier ce problème d'ordre d'affichage des bits en recourant à la version récursive suivante :
Notes :
Beaucoup de langages de programmation offrent directement le moyen d'afficher en binaire une valeur entière. Le but de cet exercice n'est bien sûr pas d'utiliser de tels moyens, mais bien de programmer par vous-même l'algorithme de conversion.
On suppose ici que le nombre entier à convertir est assez petit
pour être correctement représenté sur un int du
langage de programmation utilisé. Il n'est pas question dans cet
exercice de gérer la représentation mémoire de nombres entiers
plus grands que ce que permet le langage de programmation utilisé.
La conversion réciproque (binaire vers décimal positif) se fait simplement en ajoutant la puissance de 2 correspondant à chaque '1' présent dans l'écriture binaire.
On peut par exemple utiliser l'algorithme suivant :
initialiser r à 0 et p à 1
En allant du dernier bit au premier (sens inverse de lecture) :
Si le bit est à 1, augmenter r de p (r <-- r + p)
multiplier p par 2
On peut maintenant s'intéresser aux nombres négatifs, représenté en binaire en « complément à 2 ». Pour simplifier ici, on ne fixera pas la taille de la représentation binaire, mais on ajoutera simplement le bit de signe au début (= à gauche) de l'écriture binaire minimale nécessaire pour représenter le nombre (exemples ci-dessous).
Commencez pour cela par écrire une fonction qui retourne le complément à 2 d'une écriture binaire.
Le plus simple pour cela est d'inverser tous les bits à gauche du 1 le plus à droite (et laisser le reste inchangé).
Par exemple, le complément à 2 de « 100110100 » est « 011001100 » (notez que la partie soulignée est inchangée et le reste inversé).
Une fois une telle fonction à disposition, il suffit d'appliquer les conversions précédentes si le nombre est positif (bit de signe à 0) et d'appliquer le complément à 2 à la conversion de leur opposé si le nombre est négatif.
On prêtera cependant attention au fait de rajouter un bit supplémentaire (bit de signe) au début des écritures binaires non signées.
Commencez par tester avec des valeurs simples (puissances de 2).
L'écriture binaire sans bit de signe de 42 est 101010.
L'écriture binaire signée de 42 est 0101010.
L'écriture binaire signée de -42 est 1010110.
dec2bin.cc
Dec2Bin.java
[retour à la liste des exercices]
Implémenter les recherches linéaire et dichotomique ;
Réaliser la supériorité de la recherche dichotomique, possible seulement avec une liste triée au préalable.
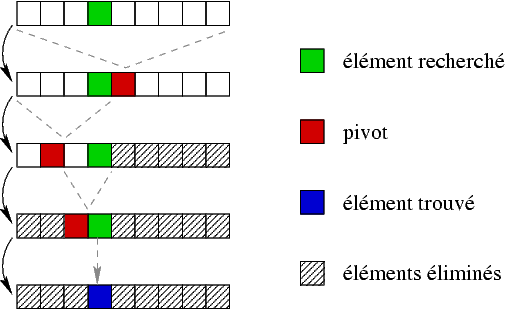
Pour illustrer la recherche par dichotomie d'un élément dans une liste ordonnée, nous allons jouer à un petit jeu :
Pensez très fort à un nombre entre 0 et 100...
voilà !
L'ordinateur doit maintenant le trouver...
Pour ce faire, il pourrait énumérer tous les nombres les uns après les
autres jusqu'à avoir la bonne réponse (recherche linéaire).
Mais, vous en conviendrez aisément, ce n'est pas une méthode très efficace...
Une autre méthode (plus efficace) est la méthode dite « par dichotomie
» : on réduit le champ de recherche à chaque étape et on
recommence la recherche sur le nouvel intervalle.
Mais ce type de recherche n'est possible que dans une liste ordonnée, ce qui est bien le cas ici (les nombres possibles entre 0 et 100).
On commence avec le domaine complet, puis on choisit un pivot (point central du domaine de recherche). En fonction de la comparaison de ce pivot avec l'élément recherché, plusieurs cas de figures peuvent se présenter :

Définissez une fonction cherche() qui prend en paramètre deux entiers, bornes inférieure et supérieure du domaine de recherche (0 et 100 dans notre exemple), et qui retourne un entier correspondant à la valeur trouvée (ou la borne inférieure en cas d'erreur).
Cette fonction devra choisir un pivot au milieu de l'intervalle ou s'arrêter, avec un message d'erreur, si l'intervalle est vide, proposer le pivot à l'utilisateur (exemple ci-dessous), puis en fonction de la réponse de celui-ci (<, > ou =) s'appeler elle-même sur le nouvel intervalle ainsi déterminé, ou arrêter la recherche.
MIN et MAX) ;
cherche() et affichez le résultat trouvé.
Pensez à un nombre entre 1 et 100. Le nombre est il <, > ou = à 50 ? < Le nombre est il <, > ou = à 25 ? > Le nombre est il <, > ou = à 37 ? < Le nombre est il <, > ou = à 31 ? > Le nombre est il <, > ou = à 34 ? < Le nombre est il <, > ou = à 32 ? > Le nombre est il <, > ou = à 33 ? = Votre nombre était 33.
dichotomie.cc
Dichotomie.java
[retour à la liste des exercices]
implémenter le tri par insertion et le tri par fusion; réaliser la supériorité du tri par fusion
[retour à la liste des exercices]
implémentation de la récursivité
On dispose d'un plateau de jeu de tour de Hanoï constitué de 3 piliers (cf le cours ICC, leçon I.2).
N disques de diamètres décroissants sont placés sur le premier pilier, Les deux autres étant vides.
Exemple avec N=4 :
- | | --- | | ----- | | ------- | | ###########################
L'objectif est de déplacer les N disques du premier au dernier pilier en utilisant si nécessaire le pilier du centre comme pilier de stockage.
On ne peut déplacer qu'un seul disque à la fois, et il faut
respecter
à tout moment la contrainte suivante :
aucun
disque ne peut être posé sur un disque plus petit que lui.
Soit void hanoi(n, A, B) la fonction qui déplace
les n disques du dessus du pilier A vers le pilier
B (A et B sont des chiffres entre 0 et 2).
Cette fonction peut être écrite de façon récursive avec les constatations suivantes :
n=0, il n'y a rien à faire.
n-1 disques, on
sait le
résoudre pour n disques (n > 0).
n-1 premiers disques du pilier A au
pilier C (avec C != A et C != B).
nième disque de A à
B.
n-1 disques de C à B.
(voir le cours ICC I.2 pour plus de détails si nécessaire)
Il faut commencer par définir les structures de données qui vont
être utilisées pour représenter le jeu.
On va pour cela représenter les disques par leur rayon :
définissez par exemple
Disque comme étant un entier non signé (rayon du disque) ;
PAS_DE_DISQUE comme étant le Disque de rayon nul (c.-à-d. donc simplement la constante 0 ;
N représentant
la taille initiale de la tour à déplacerLe jeu sera alors représenté comme un tableau de 3 piliers,
chaque pilier étant un tableau dynamique de Disques.
Définissez ensuite 3 fonctions principales :
void init(Jeu& jeu);, qui initialise le jeuvoid affiche(const Jeu& jeu); ;
hanoi (prototype donné plus tard
ci-dessous), qui résout (récursivement) le problème du déplacement d'une tour.
int main()
{
Jeu monjeu;
init(monjeu);
affiche(monjeu);
hanoi(N, 0, 2, monjeu);
return 0;
}
La fonction d'initialisation met simplement un disque de
rayon i à la i-ème position du premier
pilier, et PAS_DE_DISQUE à toutes les positions
des autres piliers.
Pour la fonction qui affiche l'état du jeu (voir l'exemple de déroulement ci-dessous), je vous propose d'adopter une approche modulaire (décomposition de la tâche en sous-tâches) :
void affiche(const Disque& d);, pour afficher un disque ;
void affiche(char c, unsigned int n = 1);, affichant n caractères identiques consécutivement.
Écrivez enfin la fonction
void hanoi(unsigned int n, unsigned int origine, unsigned int destination, Jeu& jeu)de sorte qu'elle déplace
n disques de la tour origine au
pilier destination, en utilisant
les principes présentés plus haut.
On utilisera également une approche modulaire pour la fonction
hanoi :
void deplace(Pilier& origine, Pilier& destination)qui, si le déplacement est valide, déplace le premier disque du pilier
origine au pilier destination.
définir une fonction
unsigned int autre(unsigned int p1, unsigned int p2)qui, étant donné les numéros de deux piliers (
p1 et p2), détermine le numéro du troisième
pilier.
autre(0, 2) vaut 1,
autre(2, 1) vaut 0, etc.
Indice : utilisez la somme p1+p2, sachant que la sommes des 3 numéros de piliers fait toujours 3.
Voici un exemple pour N=3 :
- | | --- | | ----- | | ################# | | | --- | | ----- | - ################# | | | | | | ----- --- - ################# | | | | - | ----- --- | ################# | | | | - | | --- ----- ################# | | | | | | - --- ----- ################# | | | | | --- - | ----- ################# | | - | | --- | | ----- #################
Hanoi.java
[retour à la liste des exercices]
Mettre en pratique la programmation dynamique.
[retour à la liste des exercices]
exemple de problème difficile (c.-à-d. dans NP), résolution exhaustive versus méthodes d'approximation (algorithme glouton pour commencer)
Le problème dit « du sac à dos » consiste à trouver, parmi un ensemble initial d'objets ayant chacun un poids et une valeur, quels objets mettre dans le sac de sorte que celui-ci ai une valeur maximale, mais ne pèse pas plus qu'un poids fixé au départ.
Par exemple, on chercher à remplir au mieux (valeur maximale) le sac à dos à partir des objets suivants, mais sans dépasser un poids total de 9 kg :
A noter que c'est bien la contrainte du poids maximal à ne pas dépasser qui rend ce problème « intéressant ». Sans une telle contrainte, il suffirait de tout mettre dans le sac pour maximiser sa valeur !
Ce problème « du sac à dos » est un problème NP-complet, c.-à-d. qu'à ce jour on ne connaît pas de meilleur algorithme pour le résoudre que celui qui consiste à essayer toutes les solutions.
Face à ce genre de problèmes, on peut alors chercher à ne pas le résoudre de façon optimale, mais utiliser un algorithme plus efficace que la recherche exhaustive, mais qui ne donnera qu'une solution approximative (une bonne solution mais qui n'est pas garantie pour être la meilleure).
Par exemple, un algorithme simple non optimal consiste à simplement remplir le sac avec les objets dans l'ordre dans lequel ils sont donnés/posés sur la table, si c'est possible (c.-à-d. ajouter l'objet ne fait pas dépasser le poids maximal autorisé).
Un autre algorithme simple non optimal consiste remplir le sac en mettant l'objet le plus lourd en premier si c'est possible, puis ensuite le 2e objet le plus lourd si c'est possible, etc. C'est le même algorithme que le précédent mais où l'on a au préalable trié les objets par poids décroissant. On appelle cet algorithme, un algorithme « glouton » car il « veut » consommer le plus en premier.
Si l'on applique le premier algorithme à l'exemple ci-dessus :
Au final, on arrive avec un poids total = 6 kg et une valeur totale de 11.
Si l'on applique l'algorithme glouton :
Au final, on arrive avec un poids total = 8 kg et une valeur totale de 13, ce qui est déjà mieux.
Mais la solution optimale consiste ici à prendre la boîte et le paquet. Le poids total est de 9 kg et la valeur totale de 15.
Le but est de programmer ces trois algorithmes. Commencez pour cela par représenter la liste des objets possibles, par exemple comme un ensemble de paires de valeurs.
Implémentez ensuite la recherche naïve (premier algorithme) dans une fonction qui prend en paramètres une liste d'objets et un poids maximal. Cette fonction affichera la valeur maximale trouvée et le poids restant libre dans le sac (avec notre exemple, elle afficherait : « valeur : 11, poids restant : 3 kg »).
Implémenez ensuite l'algorithme glouton en :
La partie la plus difficile est la recherche exacte. Celle-ci se fera de façon récursive en considérant le meilleur résultat des deux solutions consistant à prendre ou non le premier objet de la liste puis rechercher sur la suite de la liste des objets.
Plus précisément : écrire une fonction (récursive) qui prend une liste d'objets, un index de début et un poids maximum et qui
knapsack.cc
[retour à la liste des exercices]
comprendre la condition de Nyquist; comprendre la formule d'interpolation; observer l'effet stroboscopique
[retour à la liste des exercices]
Comprendre la formule mathématique du filtre à moyenne mobile;
Observer la régularisation des données, ainsi que le décalage dans le temps
En cours ICC, nous avons vu le filtre à moyenne mobile d'un signal continu (calcul par une intégrale). Ici, nous vous propoposon de voir comment calculer la moyenne mobile « discrète » d’un signal échantillonné, c.-à-d. une approximation par somme de Riemann de la version continue vue en cours ICC.
Un signal échantillonné n'est qu'un ensemble fini de valeurs, un tableau de valeur en programmation. Sa moyenne mobile n'est autre que la moyenne d'un nombre fixe de ces valeurs.
Soit Tc ce nombre fixe de valeurs sur lesquelles ont veut faire la moyenne (c'est un nombre entier). Par exemple, Tc = 3.
La valeur à l'échantillon n (c.-à-d. au temps t = n Te) du filtre à moyenne mobile est définie comme la moyenne des Tc valeurs précédentes du signal Y :
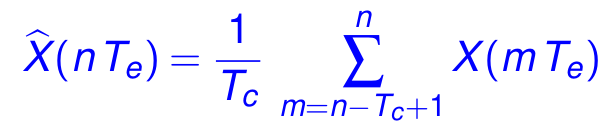
Par exemple, si X vaut : 15.1, 14.8, 13.7, 12.6, 13.8, 14.1, et que Tc = 3, alors la valeur du signal filtré vaut :
14.53 (moyenne de 15.1, 14.8 et 13.7),
13.70 (moyenne de 14.8, 13.7 et 12.6),
13.37 (moyenne de 13.7, 12.6 et 13.8),
et 13.50 (moyenne de 12.6, 13.8 et 14.1).
Un signal échantillonné sera donc simplement représenté comme un tableau de valeurs. La fonction « _filtre à moyenne mobile » prend alors simplement en paramètres le signal d'entrée (tableau de valeurs) et la taille de la fenêtre (Tc) et retourne le signal filtré, c.-à-d. un autre tableau de valeurs.
A noter que dans la définition précédente, la première valeur du signal filtré ne peut être fourni qu'après avoir eu au moins Tc, les valeurs précédentes n'étant pas définies.
Pour simplifier, nous allons ici décider que le signal filtré à la même taille que le signal d'entrée et que ses Tc - 1 valeurs initiales sont identiques à celle du signal de départ (choix arbitraire simple à implémenter). Voir l'exemple ci-dessous.
Implémentez la fonction qui effecture ce filtrage à moyenne mobile, puis, pour plus facilement exploiter le résultat de votre programme, implémentez également une fonction qui prend deux tableaux de valeurs en argument et les affiche allignés comme dans l'exemple ci-dessous.
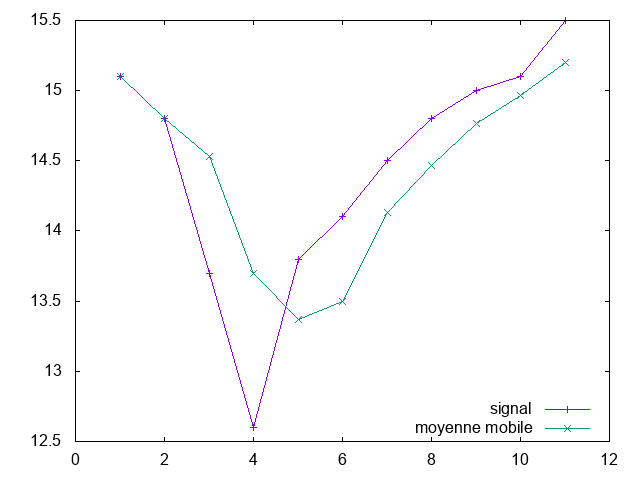
Si par exemple le signal échantillonné de départ a les valeurs :
15.1, 14.8, 13.7, 12.6, 13.8, 14.1, 14.5, 14.8, 15.0, 15.1, 15.5
alors le programme devra afficher :
# signal moving average 15.1 15.1 14.8 14.8 13.7 14.5333 12.6 13.7 13.8 13.3667 14.1 13.5 14.5 14.1333 14.8 14.4667 15 14.7667 15.1 14.9667 15.5 15.2
gnuplotLe format utilisé pour l'affichage permet d'utiliser le logiciel de dessins de courbes gnuplot de façon simple :
> :
./moving_average > resultat.txt
gnuplot
plot "resultat.txt" u 1 w linesp t "signal", "resultat.txt" u 2 w linesp t "moyenne mobile"
Vous devriez alors avoir la figure suivante à l'écran :
Note : si la légende n'est pas au bon endroit, dans gnuplot donnez simplement la commande :
set key bottom right; replot
moving_average.cc
[retour à la liste des exercices]
se familiariser avec la notion d'entropie
On se propose ici de calculer l'entropie
Une distribution de probabilités est simplement un tableau de nombres réels compris entre 0 et 1 et dont la somme est 1.0
Définissez un type Distribution pour représenter une distribution de probabilités.
L'entropie d'une distribution de probabilités est l'opposé de la somme de ses valeurs multipliées par leur logarithme. Si l'on veut l'exprimer en bits, on prendra le logarithme en base 2 :
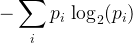
Définissez une fonction entropie qui calcule l'entropie d'une distribution de probabilités.
Attention à traiter correctement le cas p=0, pour lequel p log(p) vaut 0.
Dans le cours ICC, nous avons défini l'entropie d'une chaîne de caractères comme l'entropie de la distribution de probabilité empirique, i.e. la distribution de probabilité résultant du décompte du nombre de chacune des lettres dans cette même chaîne.
Il nous faut donc commencer par calculer cette distribution. Définissez pour cela une fonction calcules_probas qui reçoit une chaîne de caractères et retourne la distribution de probabilité de ses lettres : pour chacune des lettres, on compte le nombre de fois qu'elle apparaît dans la chaîne puis on divise par le nombre total de lettre.
Pour rendre cette fonction un tout petit peu plus générale :
true, prendra en compte également les espaces (i.e. 27 lettres) alors que sinon le calcul est fait comme dans le cours ICC en ignorant les espaces ;
toupper() de la bibliothèque cctype qui retourne la version majuscule (ou lui-même) d'une lettre (alphabétique) reçue en paramètre ; on utilisera par ailleurs au préalable la fonction isalpha (de la même bibliothèque cctype) pour déterminer si un caractère donnée est une lettre de l'alphabet ou non.Pour calculer cette distribution de probabilité empirique, je vous conseille de tout d'abord créer un tableau de taille fixe de 27 nombre pour compter le nombre d'occurrence de chacune des vingt-sept lettre. Utilisez ensuite ce tableau pour construire une distribution de probabilité avec uniquement les lettres qui apparaissent, i.e. les probabilités non nulles (cf exemple ci-dessous).
Terminez en définissant une fonction entropie qui reçoit en paramètre une chaîne de caractères et retourne son entropie (i.e. l'entropie de sa distribution empirique des lettres).
Voici quelques entropies qui vous permettrons de tester votre code :
| distribution | entropie (en bit) |
|---|---|
| { 0.0, 0.1 } | 0 |
| { 0.3, 0.7 } | 0.881291 |
| { 0.5, 0.5 } | 1 |
| { 0.1, 0.2, 0.3, 0.4 } | 1.84644 |
| { 0.25, 0.25, 0.125, 0.0625, 0.0625, 0.0625, 0.0625, 0.0625, 0.0625 } | 2.875 |
Et pour rappel (cf cours ICC), l'entropie de la chaîne « IL FAIT BEAU A IBIZA », en ignorant les espaces, est de 2.875 bit, sa distribution de probabilités étant la dernière donnée ci-dessus.
[retour à la liste des exercices]
exemple d'algorithme glouton, et pourtant optimal